Fractal Dimension
After the previous post I thought it would be interesting to compare the topological dimension to the fractal dimension as it is presented in Kenneth Falconer’s Fractal Geometry. A fractal is commonly defined as an object which has a Hausdorff-Besicovitch dimension strictly greater than its topological dimension.
Quoting from the book:
Hausdorff measure
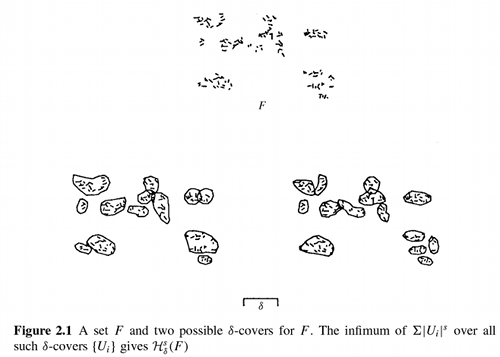
Recall that if \(U\) is any non-empty subset of n-dimensional Euclidean space, \(R^n\), the diameter of \(U\) is defined as \(|U| = sup\{|x-y|: x,\ y\ \epsilon\ U\}\), i.e. the greatest distance apart of any pair of points in \(U\). If \(\{U_i\}\) is a countable (or finite) collection of sets of diameter at most \(\delta\) that cover \(F\), i.e. \(F \subset \bigcup_{i=1}^\infty\ U_i\) with \(0 \leq |U_i| \leq \delta\) for each \(i\), we say that \(\{U_i\}\) is a \(\delta\)-cover of \(F\).
Suppose that \(F\) is a subset of \(R^n\) and \(s\) is a non-negative number. For any \(\delta \gt 0\) we define
| \(H_{\delta}^s(F) = inf\left(\sum_{i=0}^\infty | U_i | ^s \right)\): \(\{U_i\}\) is a \(\delta\)-cover of \(F\) |
Thus we look at all covers of \(F\) by sets of diameter at most \(\delta\) and seek to minimize the sum of the \(s\)th powers of the diameters. As \(\delta\) decreases, the class of permissible covers of \(F\) is reduced. Therefore, the infimum \(H_{\delta}^s(F)\) increases, and so approaches a limit as \(delta \to 0\). We write
\(H^s(F) = \lim_{\delta \to 0} H_{\delta}^s(F)\)
This limit exists for any suybset \(F\) of \(R^n\), though the limiting value can be (and usually is) \(0\) or \(\infty\). We call \(H^s(F)\) the s-dimensional Hausdorff measure of F.
(…)
Hausdorff dimension
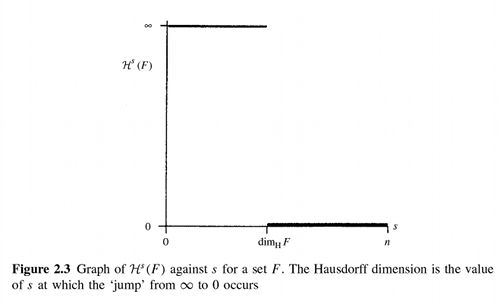
If \(t \gt s\) and \(\{U_i\}\) is a \(\delta\)-cover of \(F\) we have
| \(\sum_i | U_i | ^t \leq \sum_i | U_i | ^{t-s} | U_i | ^s \leq \delta^{t-s} \sum_i | U_i | ^s\) |
so, taking infima, \(H_{\delta}^t(F) \leq \delta^{t-s} H_{\delta}^s(F)\). Letting \(\delta \to 0\) we see that if \(H^s(F) \lt \infty\) then \(H^t(F) = 0\) for \(t \gt s\). Thus a graph of \(H^s(F)\) against \(s\) shows that there is a critical value of \(s\) at which \(H^s(F)\) ‘jumps’ from \(\infty\) to \(0\). This critical value is called the Hausdorff dimension of \(F\), and written \(dim_H F\); it is defined for any set \(F \subset R^n\). (Note that some authors refer to Hausdorff dimension as Hausdorff-Besicovitch dimension). Formally
\(dim_H F = inf\{s \geq 0\ :\ H^s(F) = 0\} = sup\{s\ :\ H^s(F) = \infty\}\)