« V8-GL Update
Outside In »

Drawing Trees

Posted in: visualization
While trying to fix a SpaceTree layout issue for version 1.1.2 of the JavaScript InfoVis Toolkit I found a Microsoft Research paper that describes a functional programming approach for rendering trees in an aesthetically pleasing way. But what is aesthetically pleasing? Andrew J. Kennedy takes Radack and Walker rules:
  1. Two nodes at the same level should be placed at least a given distance apart.
  2. A parent should be centred over its o?spring.
  3. Tree drawings should be symmetrical with respect to re?ection a tree and its mirror image should produce drawings that are re?ections of each other. In particular, this means that symmetric trees will be rendered symmetrically.
  4. Identical subtrees should be rendered identically their position in the larger tree should not a?ect their appearance.
  5. Trees should be as narrow as possible without violating these rules
In order to calculate nodes' positions Kennedy takes a "bottom-up" approach: Starting from the root node, draw for each node all its subtrees without breaking any rules. Fit these subtrees together without changing their shape, and also without breaking rules 1 and 3 (i.e do not break symmetry and avoid cluttering/overlapping of nodes). Finally, center their parent above them like specified in rule 2. The "fitting" of the subtrees is calculated by operating on subtrees extents. A subtree extent is a data structure containing the relative coordinates of the boundary of a subtree. 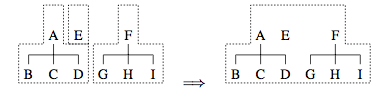One frequent operation between extents is merging: Other operations involve setting the distance between two extents, translating extents, etc.

Implementation

Kennedy implements this algorithm in Standard ML. I made a JavaScript adaptation. I like the Standard ML version a lot more; in this case rich typing makes very elegant code. Here's my code implementation, in case you want to compare it to Kennedy's. My version takes into account different tree layouts (left, right, bottom, top), siblings and subtrees offsets and different node sizes as opposed to Kennedy's version. 
function movetree(node, prop, val, orn) {
   var p = (orn == "left" || orn == "right")? "y" : "x";
   node[prop][p] += val;
 };

 function moveextent(extent, val) {
     var ans = [];
     $each(extent, function(elem) {
         elem = slice.call(elem);
         elem[0] += val;
         elem[1] += val;
         ans.push(elem);
     });
     return ans;
 };

 function merge(ps, qs) {
   if(ps.length == 0) return qs;
   if(qs.length == 0) return ps;
   var p = ps.shift(), q = qs.shift();
   return [[p[0], q[1]]].concat(merge(ps, qs));
 };

 function mergelist(ls, def) {
     def = def || [];
     if(ls.length == 0) return def;
     var ps = ls.pop();
     return mergelist(ls, merge(ps, def));
 };

 function fit(ext1, ext2, subtreeOffset, siblingOffset, i) {
     i = i || 0;
     if(ext1.length <= i ||
        ext2.length <= i) return 0;

     var p = ext1[i][1], q = ext2[i][0];
     return Math.max(fit(ext1, ext2, subtreeOffset, siblingOffset, ++i) + subtreeOffset,
                 p - q + siblingOffset);
 };

 function fitlistl(es, subtreeOffset, siblingOffset) {
   function $fitlistl(acc, es, i) {
       i = i || 0;
       if(es.length <= i) return [];
       var e = es[i], ans = fit(acc, e, subtreeOffset, siblingOffset);
       return [ans].concat($fitlistl(merge(acc, moveextent(e, ans)), es, ++i));
   };
   return $fitlistl([], es);
 };

 function fitlistr(es, subtreeOffset, siblingOffset) {
   function $fitlistr(acc, es, i) {
       i = i || 0;
       if(es.length <= i) return [];
       var e = es[i], ans = -fit(e, acc, subtreeOffset, siblingOffset);
       return [ans].concat($fitlistr(merge(moveextent(e, ans), acc), es, ++i));
   };
   es = slice.call(es);
   var ans = $fitlistr([], es.reverse());
   return ans.reverse();
 };

 function fitlist(es, subtreeOffset, siblingOffset) {
    var esl = fitlistl(es, subtreeOffset, siblingOffset),
        esr = fitlistr(es, subtreeOffset, siblingOffset);
    for(var i = 0, ans = []; i < esl.length; i++) {
        ans[i] = (esl[i] + esr[i]) / 2;
    }
    return ans;
 };

 function design(graph, node, prop, config) {
     var orn = config.orientation;
     var auxp = ['x', 'y'], auxs = ['width', 'height'];
     var ind = +(orn == "left" || orn == "right");
     var p = auxp[ind], notp = auxp[1 - ind];

     var cnode = config.Node;
     var s = auxs[ind], nots = auxs[1 - ind];

     var siblingOffset = config.siblingOffset;
     var subtreeOffset = config.subtreeOffset;

     var GUtil = Graph.Util;
     function $design(node, maxsize, acum) {
         var sval = (cnode.overridable && node.data["$" + s]) || cnode[s];
         var notsval = maxsize || ((cnode.overridable && node.data["$" + nots]) || cnode[nots]);

         var trees = [], extents = [], chmaxsize = false;
         var chacum = notsval + config.levelDistance;
         GUtil.eachSubnode(node, function(n) {
             if(n.exist) {
                 if(!chmaxsize)
                    chmaxsize = getBoundaries(graph, config, n._depth);

                 var s = $design(n, chmaxsize[nots], acum + chacum);
                 trees.push(s.tree);
                 extents.push(s.extent);
             }
         });
         var positions = fitlist(extents, subtreeOffset, siblingOffset);
         for(var i=0, ptrees = [], pextents = []; i < trees.length; i++) {
             movetree(trees[i], prop, positions[i], orn);
             pextents.push(moveextent(extents[i], positions[i]));
         }
         var resultextent = [[-sval/2, sval/2]].concat(mergelist(pextents));
         node[prop][p] = 0;

         if (orn == "top" || orn == "left") {
            node[prop][notp] = acum;
         } else {
            node[prop][notp] = -acum;
         }
         return {
           tree: node,
           extent: resultextent
         };
     };
     $design(node, false, 0);
 };
« V8-GL Update
Outside In »
Comments
blog comments powered by Disqus